初三中考数学二次函数较难题解析

概要：初三中考数学二次函数较难题解析是由www.kgf8.com中考网整理的，主要是从二次函数图象考点、二次函数解析式等中考要点题型解析，供大家冲刺中考数学参考，希望本初三中考数学二次函数较难题解析可以帮到考生备考!二次函数的图像考点：开口方向，对称轴，顶点，与x轴的交点，与y轴的交点.二次函数：y=ax2+bx+c(a，b，c是常数，a≠0)一般式：y=ax2+bx+c，三个点顶点式：y=a(x-h)2+k，顶点坐标对称轴顶点坐标顶点坐标(h，k)a b c作用分析│a│的大小决定了开口的宽窄，│a│越大，开口越小，│a│越小，开口越大，a，b的符号共同决定了对称轴的位置，当b=0时，对称轴x=0，即对称轴为y轴，当a，b同号时，对称轴x=-<0，即对称轴在y轴左侧，当a，b异号时，对称轴x=->0，即对称轴在y轴右侧，(左同右异y轴为0)c的符号决定了抛物线与y轴交点的位置，c=0时，抛物线经过原点，c>0时，与y轴交于正半轴;c<0时，与y轴交于负半轴，以上a，b，c的符号与图像的位置是共同作用的，也可以互相推出.交点式：y=a(

初三中考数学二次函数较难题解析,标签：九年级数学代数练习,http://www.kgf8.com

　　初三中考数学二次函数较难题解析是由www.kgf8.com中考网整理的，主要是从二次函数图象考点、二次函数解析式等中考要点题型解析，供大家冲刺中考数学参考，希望本初三中考数学二次函数较难题解析可以帮到考生备考!

　　二次函数的图像考点：

　　开口方向，对称轴，顶点，与x轴的交点，与y轴的交点.

　　二次函数：y=ax²+bx+c(a，b，c是常数，a≠0)

　　一般式：y=ax²+bx+c，三个点

　　顶点式：y=a(x-h)²+k，顶点坐标对称轴

　　顶点坐标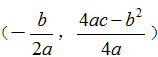

　　顶点坐标(h，k)

　　a b c作用分析

　　│a│的大小决定了开口的宽窄，│a│越大，开口越小，│a│越小，开口越大，

　　a，b的符号共同决定了对称轴的位置，当b=0时，对称轴x=0，即对称轴为y轴，当a，b同号时，对称轴x=-<0，即对称轴在y轴左侧，当a，b异号时，对称轴x=->0，即对称轴在y轴右侧，(左同右异y轴为0)

　　c的符号决定了抛物线与y轴交点的位置，c=0时，抛物线经过原点，c>0时，与y轴交于正半轴;c<0时，与y轴交于负半轴，以上a，b，c的符号与图像的位置是共同作用的，也可以互相推出.

　　交点式：y=a(x- x₁)(x- x₂)，(有交点的情况)

　　与x轴的两个交点坐标x₁，x₂

　　对称轴为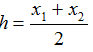

　一、二次函数解析式及定义型问题(顶点式中考要点)

　　1.把二次函数的图象向左平移2个单位，再向上平移1个单位，所得到的图象对应的二次函数关系式是y=(x+1)²-2则原二次函数的解析式________________。

　　2.二次函数的图象顶点坐标为(2，1)，形状开品与抛物线y=-2x²相同，这个函数解析式为________。

　　点击下载：初三中考数学二次函数较难题解析

　　初三中考数学二次函数较难题解析，是由www.kgf8.com中考网提供，希望本篇资料对大家有帮助，更多资料请点击查看www.kgf8.com中考网。

　 上一篇：2014中考数学经典轴对称题选编