2017中考数学二次函数专题复习

概要：2013中考数学二次函数专题复习是由www.kgf8.com中考网整理的，主要包括二次函数的图象和性质和二次函数的图像与系数的关系这几个知识点，每个知识点都包含经典例题解析、针对性训练，供大家参考练习，希望2013中考数学二次函数专题复习能够帮助大家对中考数学二次函数的应用把握得更准确。2013中考数学二次函数专题复习考点1：二次函数的图象和性质一、考点讲解：1.二次函数的定义：形如y=ax2+bx+c(a≠0，a，b，c为常数)的函数为二次函数.2.二次函数的图象及性质：⑴ 二次函数y=ax2 (a≠0)的图象是一条抛物线，其顶点是原点，对称轴是y轴;当a>0时，抛物线开口向上，顶点是最低点;当a<0时，抛物线开口向下，顶点是最高点;a越小，抛物线开口越大.y=a(x-h)2+k的对称轴是x=h，顶点坐标是(h，k)。注意：分析二次函数增减性时，一定要以对称轴为分界线。首先要看所要分析的点是否是在对称轴同侧还是异侧，然后再根据具体情况分析其大小情况。3.图象的平移：将二次函数y=ax2 (a≠0)的图象进行平移，可得到y=ax2+c

2017中考数学二次函数专题复习,标签：中考数学复习资料大全,中考总复习,http://www.kgf8.com

　　2013中考数学二次函数专题复习是由www.kgf8.com中考网整理的，主要包括二次函数的图象和性质和二次函数的图像与系数的关系这几个知识点，每个知识点都包含经典例题解析、针对性训练，供大家参考练习，希望2013中考数学二次函数专题复习能够帮助大家对中考数学二次函数的应用把握得更准确。

　　2013中考数学二次函数专题复习

　　考点1：二次函数的图象和性质

　　一、考点讲解：

　　1.二次函数的定义：形如y=ax²+bx+c　(a≠0，a，b，c为常数)的函数为二次函数.

　　2.二次函数的图象及性质：

　　⑴ 二次函数y=ax² (a≠0)的图象是一条抛物线，其顶点是原点，对称轴是y轴;当a>0时，抛物线开口向上，顶点是最低点;当a<0时，抛物线开口向下，顶点是最高点;a越小，抛物线开口越大.y=a(x-h)2+k的对称轴是x=h，顶点坐标是(h，k)。

　　

　　注意：分析二次函数增减性时，一定要以对称轴为分界线。首先要看所要分析的点是否是在对称轴同侧还是异侧，然后再根据具体情况分析其大小情况。

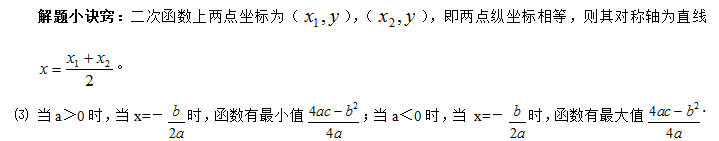
　　3.图象的平移：将二次函数y=ax² (a≠0)的图象进行平移，可得到y=ax²+c，y=a(x-h)²，y=a(x-h)²+k的图象.

　　⑴ 将y=ax²的图象向上(c>0)或向下(c< 0)平移|c|个单位，即可得到y=ax²+c的图象.其顶点是(0,c)，形状、对称轴、开口方向与抛物线y=ax2相同.

　　⑵ 将y=ax²的图象向左(h<0)或向右(h>0)平移|h|个单位，即可得到y=a(x-h)²的图象.其顶点是(h，0)，对称轴是直线x=h，形状、开口方向与抛物线y=ax2相同.

　　⑶ 将y=ax²的图象向左(h<0)或向右(h>0)平移|h|个单位，再向上(k>0)或向下(k<0)平移|k|个单位，即可得到y=a(x-h)² +k的图象，其顶点是(h，k)，对称轴是直线x=h，形状、开口方向与抛物线y=ax2相同.

　　注意：二次函数y=ax² 与y=-ax² 的图像关于x轴对称。平移的简记口诀是“上加下减，左加右减”。

　　一、 经典考题剖析：

　　【考题1】.抛物线y=-4(x+2)²+5的对称轴是______

　　解：x=-2 点拨：抛物线y=a(x-h)²+k的对称轴为x=h.

　　【考题2】函数y= x2-4的图象与y 轴的交点坐标是( )

　　A.(2，0) B.(-2，0)

　　C.(0，4) D.(0，-4)

　　解：D 点拨：函数y= x²-4的图象与 y轴的交点的 横坐标为0，x=0时，y=-4，故选D.

　　点击下载：2013中考数学二次函数专题复习

　　2013中考数学二次函数专题复习，是由www.kgf8.com中考网提供的，希望本篇资料可以帮助大家，更多资料请查看www.kgf8.com中考网。

　 上一篇：2017中考数学冲刺备考策略