中学趣味数学:没有放上的数字

概要：有人把0～9这十个数字中的九个用字母代表，如上图那样放在两个三角形的每一个周围。(1)三角形各边上四个数字之和为14。(2)在第一个三角形中没有放上的数字，不同于在第二个三角形中没有放上的数字。在两个三角形中没有放上的是十个数字中的哪两个?(提示：建立一个方程，把没有放上的数字同三个角上的数字之和联系起来。(注意把三条边上的数字之和加起来时，三个角上的数字用了两次。)然后，根据可能的三个角数字之和，判定各个角上的可能的数字。最后判定放在各个角之间的数字。)答案根据(I)，(A+B+C+D)+(D+E+F+G)+(G+H+I+A)=14+14+14，即2A+2D+2C+B+C+E+F+H+I=420～9这十个数字之和为45;因此，如果以J代表没有放上的数字，则A+B+C+D+E+F+G+H+I=45-J。从第一个方程中减去第二个方程，得到：A+D+G=J-3。由于A+D+C至少等于3，而J最多等于9，只可能有以下的情况：A+D+GJ(i)36(ii)47(iii)58(iv)69于是，以下情况中必然有一种会发生：从而得到：由此可见，只有(i)和(ii)能继续补上数字而

中学趣味数学:没有放上的数字,标签：七年级数学练习题,http://www.kgf8.com

　　有人把0～9这十个数字中的九个用字母代表，如上图那样放在两个三角形的每一个周围。

　　

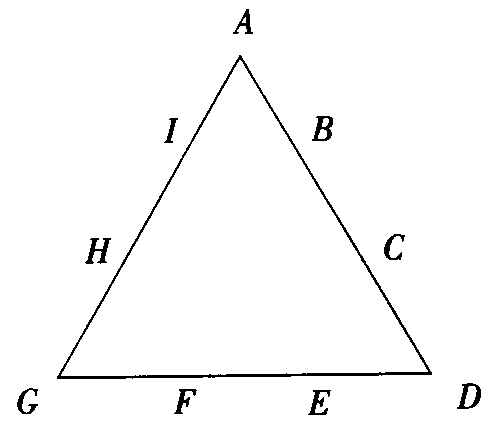
　　(1)三角形各边上四个数字之和为14。

　　(2)在第一个三角形中没有放上的数字，不同于在第二个三角形中没有放上的数字。

　　在两个三角形中没有放上的是十个数字中的哪两个?

　　(提示：建立一个方程，把没有放上的数字同三个角上的数字之和联系起来。(注意把三条边上的数字之和加起来时，三个角上的数字用了两次。)然后，根据可能的三个角数字之和，判定各个角上的可能的数字。最后判定放在各个角之间的数字。)

　　答　案

　　根据(I)，

　　(A+B+C+D)+(D+E+F+G)+(G+H+I+A)

　　=14+14+14，即

　　2A+2D+2C+B+C+E+F+H+I=42

　　0～9这十个数字之和为45;因此，如果以J代表没有放上的数字，则

　　A+B+C+D+E+F+G+H+I=45-J。

　　从第一个方程中减去第二个方程，得到：

　　A+D+G=J-3。

　　由于A+D+C至少等于3，而J最多等于9，只可能有以下的情况：

　　A+D+GJ

　　(i)

　　3

　　6

　　(ii)

　　4

　　7

　　(iii)

　　5

　　8

　　(iv)

　　6

　　9

　　于是，以下情况中必然有一种会发生：

　　

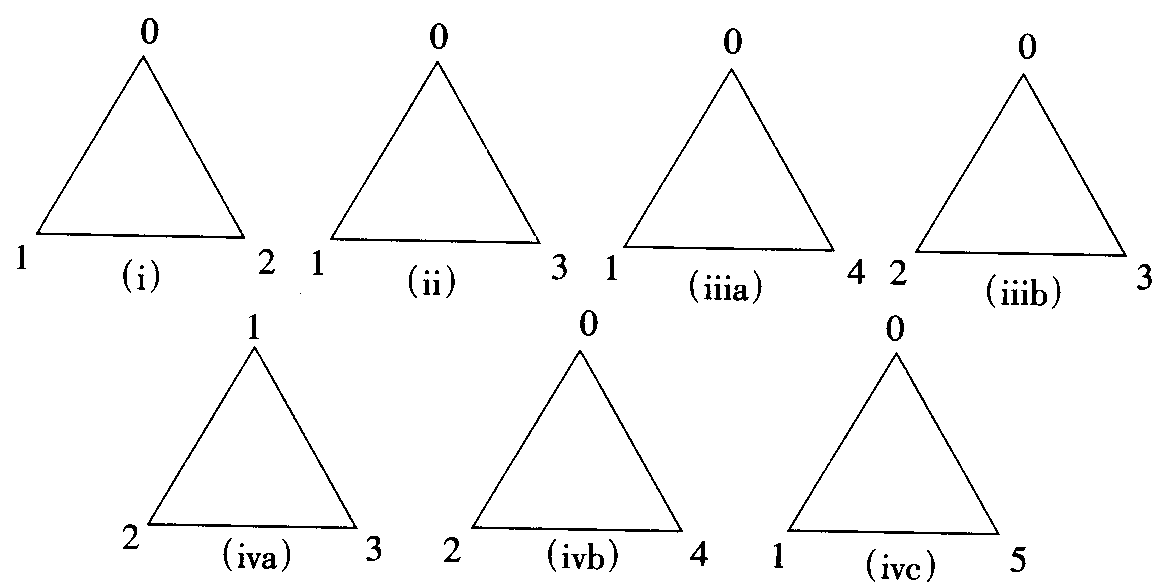
　　从而得到：

　　

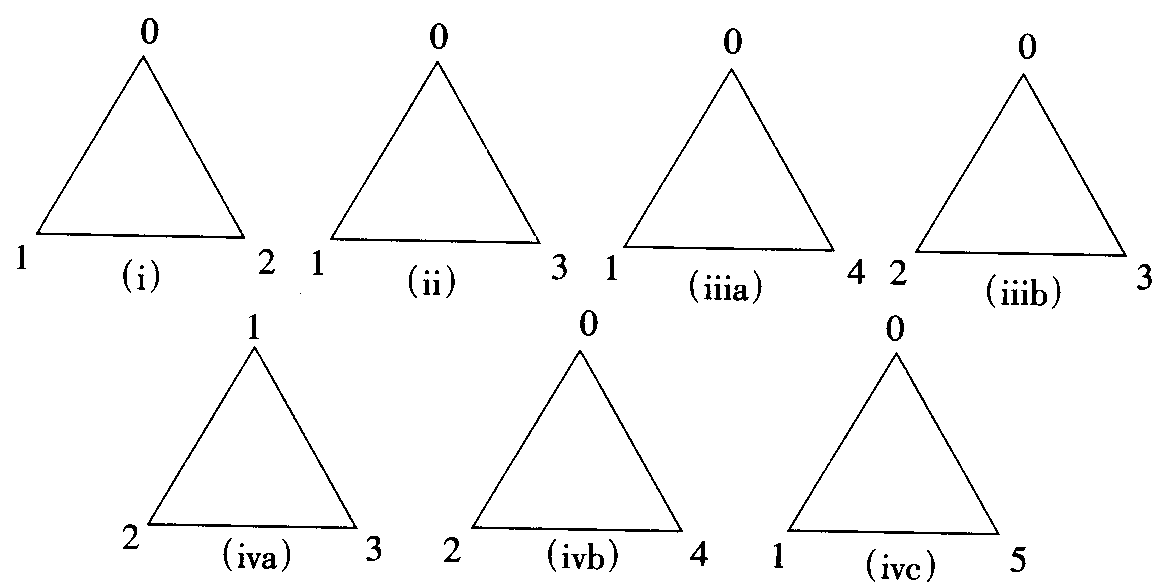
　　由此可见，只有(i)和(ii)能继续补上数字而不致发生重复，

　　即：

　　

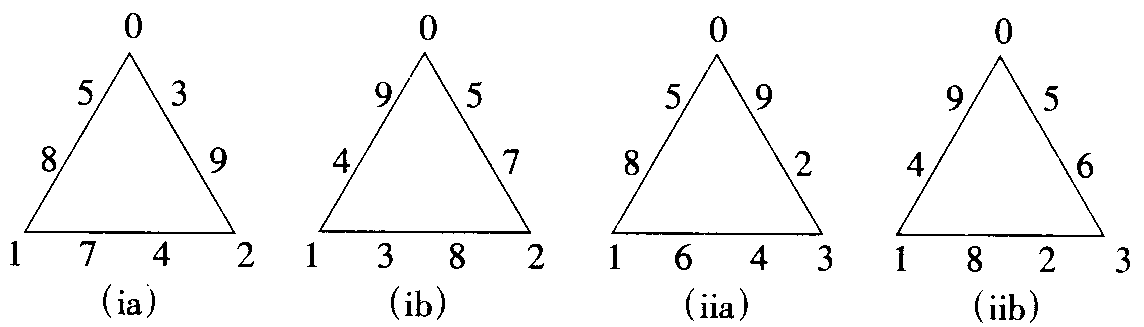
　　因此，根据(2)，6和7分别是两个三角形中没被放上的数字。

　 上一篇：中学趣味数学:蜘蛛的启示