
概要:初一数学——有理数加减的应用问题 有理数是初中数学的重要内容,其中有理数的加减在现实生活中有着广泛的应用,现举例说明.一、温度的变化例1 某地今年1月1日至4日每天的最高气温与最低气温如下表: 日 期 1月1日 1月2日 1月3日 1月4日 最高气温 5℃ 4℃ 0℃
有理数加减的应用问题,标签:七年级数学练习题,http://www.kgf8.com初一数学——有理数加减的应用问题
有理数是初中数学的重要内容,其中有理数的加减在现实生活中有着广泛的应用,现举例说明.
一、温度的变化 例1 某地今年1月1日至4日每天的最高气温与最低气温如下表: 日 期 1月1日 1月2日 1月3日 1月4日 最高气温 5℃ 4℃ 0℃ 4℃ 最低气温 0℃ ℃ ℃ ℃ 其中温差最大的是 ( ). A. 1月1日 B. 1月2日 C. 1月3日 D. 1月4日 解析: 可将同一天的气温相减,即最高气温减去最低气温,再比较大小,选D. 二、股市行情 例2 小王上周五在股市以收盘价(收市时的价格)每股25元买进某公司股票1000股,在接下来的一周交易日内,小王记下该股票每日收盘价格相比前一天的涨跌情况:(单位:元)星期 一 二 三 四 五 每股涨跌(元) +2 -0.5 +1.5 -1.8 +0.8
根据上表回答问题: (1) 星期二收盘时,该股票每股多少元? (2) 一周内该股票收盘时的最高价,最低价分别是多少? (3) 已知买入股票与卖出股票均需支付成交金额的千分之五的交易费.若小王在本周五以收盘价将全部股票卖出,他的收益情况如何? 解:(1)星期二收盘价为25+2-0.5=26.5(元/股); (2)收盘最高价为25+2-0.5+1.5=28(元/股); 收盘最低价为25+2-0.5+1.5-1.8=26.2(元/股); (3)小王的收益为 27×1000(1-5‰)-25×1000(1+5‰) =27000-135-25000-125 =1740(元), 故小王的本次收益为1740元. 三、路程的远近 例3 一跳蚤在一直线上从O点开始,第1次向右跳1个单位,紧接着第2次向左跳2个单位,第3次向右跳3个单位,第4次向左跳4个单位,……,依此规律跳下去,当它跳第100次落下时,落点处离O点的距离是 个单位.. 解析: 不妨设向左跳一个单位计为-1,向右一个单位计为+1,则跳100次落下,距离和为1-2+3-4+…+99-100=-50,所以落点处离O点的距离是50个单位. 评注: 本题若直接计算比较麻烦,而将具有相反意义的量按照这种方式数字化以后,就将问题转化为有理数运算问题,这种数学建模思想是一种重要数学思想方法. 四、走时误差的比较 例4 为了了解市场上甲、乙两种手表日走时误差的情况,从这两种手表中各随机抽取10块进行测试,两种手表日走时误差的数据如下(单位:秒)编 号 类 型 一 二 三 四 五 六 七 八 九 十 甲种手表 -3 4 2 -1 -2 -2 1 -2 2 1 乙种手表 -4 1 -2 1 4 1 -2 -1 2 -2
计算甲、乙两种手表日走时误差的平均数.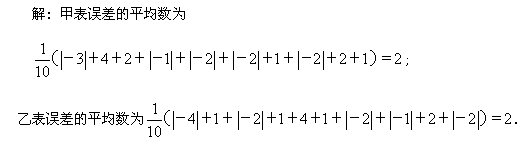
 保存 |
保存 |
 打印 |
打印 |
 关闭
关闭