中学趣味数学:隐蔽的尺寸

概要： 在城市广场的中央有一片很大的圆形憩息地。市议会拟在该地建造一个菱形浅水池。多里斯。莱特市长看到这一计划，她找来了建筑师。莱特市长：“我喜欢呈菱形的水池，用红瓷砖砌成，不知道这水池的每边有多长？”建筑师弗兰克。劳埃德。朗被问住了。朗先生：“从A至B是5米，从B至C是4米。唔，应求出BD。也许我需要应用毕达格拉斯定理。朗先生正疑惑不解，市长阁下忽然叫起来。莱特市长：“啊哈！水池每边长为9米，这是毫无疑问的。”朗先生：“我的天哪！怪不得你姓莱特（Wright）我姓朗（Wrong）呢。”有了什么好主意使这个问题迎刃而解？既是对角线又是半径莱特夫人忽然悟到水池每边即为矩形的对角线。这个矩形的另一条对角线就是圆形栖息地的半径。而矩形的两条对角线是相等的，所以水池每边边长就是圆半径的长度。半径是5+4=9米，因此水池每边也是9米，无需应用毕达格拉斯定理。你再找一种更简便的方法试试看，这样你就更能体会我们这种解法的优点。如果你仅应用毕达格拉斯定理和相似三角形，其解法一定很冗长，繁琐。但你如果

中学趣味数学:隐蔽的尺寸,标签：七年级数学练习题,http://www.kgf8.com

    在城市广场的中央有一片很大的圆形憩息地。市议会拟在该地建造一个菱形浅水池。多里斯。莱特市长看到这一计划，她找来了建筑师。莱特市长：“我喜欢呈菱形的水池，用红瓷砖砌成，不知道这水池的每边有多长？”建筑师弗兰克。劳埃德。朗被问住了。朗先生：“从A至B是5米，从B至C是4米。唔，应求出BD。也许我需要应用毕达格拉斯定理。朗先生正疑惑不解，市长阁下忽然叫起来。莱特市长：“啊哈！水池每边长为9米，这是毫无疑问的。”

　　朗先生：“我的天哪！怪不得你姓莱特（Wright）我姓朗（Wrong）呢。”有了什么好主意使这个问题迎刃而解？

　　

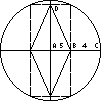
　　既是对角线又是半径

　　莱特夫人忽然悟到水池每边即为矩形的对角线。这个矩形的另一条对角线就是圆形栖息地的半径。而矩形的两条对角线是相等的，所以水池每边边长就是圆半径的长度。半径是5+4=9米，因此水池每边也是9米，无需应用毕达格拉斯定理。

　　你再找一种更简便的方法试试看，这样你就更能体会我们这种解法的优点。如果你仅应用毕达格拉斯定理和相似三角形，其解法一定很冗长，繁琐。但你如果想到下列平面几何定理：一个圆的两条内部相交的弦，一条弦的两部分之积等于另一根弦两部分之积，那么就可以得出稍微简短的解法。根据这一定理，可以求得直角三角形的高为√56，在应用毕达格拉斯定理，算出直角三角形的斜边为9。

　　有一个与此密切相关的问题，那就是诗人亨利。朗非罗在其小说《卡瓦诺》中所提出的有名的水仙花问题。当水仙花花茎垂直时，花朵伸出水面10厘米。如果把水仙花拉向一边，使花茎保持直线，花朵沾水的位置离原来的位置是21厘米，问水深多少厘米？

　　

　　要解这个问题，可以先画一张草图，此图与水池问题的图相似。我们要确定的就是x的长度。与水池问题一样，这个问题也不止一种解法。若你还记得两弦相交的定理，解这个问题是轻而易举的。

　　还有一个有趣的游泳池难题，灵机一动则迎刃而解。一条海豚位于一个圆形水池的西边A点，它笔直地游了12米，鼻子触到水边的B点，转过身后，又笔直地游了5米，到达水池边上的C点，此位置正好与水池边上的A点遥遥相对，试问如果它直接从A点游向C点，需要游多长距离？

　　啊哈！要解决这个问题只需知道下列定理：半圆上的圆周角是直角，所以三角形ABC是直角三角形。已知两直角边长分别为12米和5米，所以斜边为13米。上述问题都给我们以启示：在许多情况下，如果思路正确，几何问题的求解会变得极其容易。而要做到这一点，这取决于你是否想到了欧几里德几何的某个基本定理。

　 上一篇：中学趣味数学:谁是教授